Construct a APQR in which QR = 6cm, ∠Q = 60° and PR - PQ = 2 cm.
Given, QR = 6cm, ∠Q = 60° and PR - PQ =2 cm.
Steps of construction
(i) First, draw the base, QR = 6cm.
(ii) At the point Q, make∠XQR = 60°.
(iii) Cut line segment as QS = PR - PQ =2 cm from the line QX extended on opposite side of line segment QX.
(iv) Join SR.
(v) Now, takeS and R as the centres respectively and draw the arcs of circle of radius more than 1/2 SR.
These arcs intersect each other at point L and M.
(vi) Join LM. When LM extend, it intersects QX at P.
(vii) Join PR.
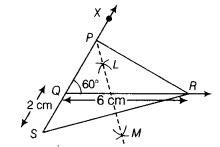
Hence, APQR is the required triangle.