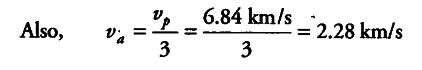A satellite is in an elliptic orbit around the earth with aphelion of 6R and perihelion of 2R, where R = 6400 km is the radius of the earth. Find eccentricity of the orbit. Find the velocity of the satellite at apogee and perigee. What should be done if this satellite has to be transferred to a circular orbit of radius 6R?
If { r }_{ a } and
{ r }_{ p } denote the distances of aphelion and perihelion of the elliptical orbit (of eccentricity) of the satellite, then from the geometry of the ellipse.
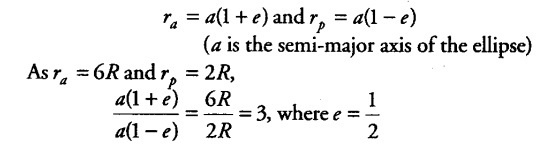
If { v }_{ a } and
{ v }_{ p } are the velocities of the satellite (of mass m) at aphelion and perihelion respectively, then from the law of conservation of angular momentum,
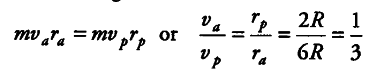
From the law of conservation of energy,
(KE + PE) at aphelion = (KE + PE) at perihelion