You have learnt, that a travelling wave in one dimension is represented by a function y=f(x, t), where x and t appear in the combination (x - vt) or (x + vt), i.e., y =f(x± vt). Is the converse true 7 That is, does every function of (x - vt) or (x + vt) represent a travelling wave 7 Examine, if the following function for y can possibly represent a travelling wave ?
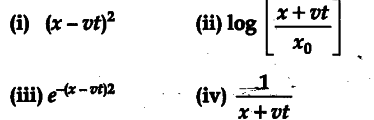
No, the converse is not true. The basic requirement for a wave function to represent a travelling wave is that for all values of x and f, wave function must have a finite value.
Out of the given functions for y only (iii) satisfies this condition. The other three functions (i), (ii) and (iv) cannot represent a travelling wave as the necessary condition is not satisfied by these functions.