In this problem we will consider the collision of two cars initially moving at right angles

Home Work Help
, ,
1

In this problem we will consider the collision of two cars initially moving at right angles. We assume that after the collision the cars stick together and travel off as a single unit. The collision is therefore completely inelastic.

Two cars of masses m1 and m2 collide at an intersection. Before the collision, car 1 was traveling eastward at a speed of v1, and car 2 was traveling northward at a speed of v2. (Figure 1) After the collision, the two cars stick together and travel off in the direction shown.

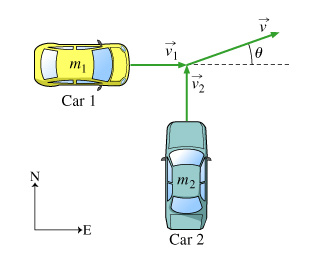
image

Part A
First, find the magnitude of Vector V, that is, the speed little v of the two-car unit after the collision. Express little v in terms of m1, m2, and the cars’ initial speeds v1 and v2.

Part B
Find the tangent of the angle theta. Express your answer in terms of the momenta of the two cars, p1 and p2.

Part C
Suppose that after the collision, tan=1; in other words, theta is 45 degrees. This means that before the collision:
Choose one:

  • The magnitudes of the momenta of the cars were equal.
  • The masses of the cars were equal.
  • The velocities of the cars were equal.

Answer:

Part A
Horizontal velocity after collision=m1v1/(m1+m2)
Verical velocity=m2v2/(m1+m2)
Magnitude of velocity=sqrt(vx2+vy2)=[1/(m1+m2)]*sqrt(m12v12+m22v22)

Part B
θ=Tan-1(p2/p1)

Part C
The magnitudes of the momenta of the cars were equal.