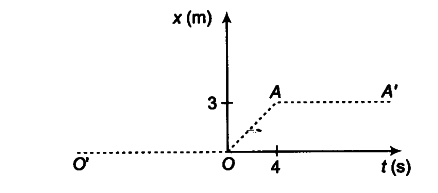
Figure below shows the position-time graph of a particle of mass 4 kg. What is the (i) force on the particle far t < 0, t > 4s, 0 < t < 4s? (ii) impulse at t = 0 and t = 4s? (Consider one-dimensional motion only).
(i) (a) For t< 0, the position-time graph is OO’, for which displacement of the particle is zero, therefore, particle is at rest at the origin. Hence, acceleration and force acting on particle will also be zero.
(b) For t > As, the position-time graph A A’ is parallel to time axis. Therefore, for t > 4 s particle remains at a fixed distance of 3 m from the origin. It means particle is at rest. Therefore, acceleration and force acting on particle will be zero.
© For 0 < t < 4 s, the position-time graph OA is a straight line inclined at an angle from time axis, which is representing uniform motion of the particle, i.e. the particle is moving with a constant velocity. Therefore, acceleration and force acting on the particle will be zero. [1 * 3]
(ii) Impulse at t = 0
(a) Impulse - change in momentum
= mv — mu = m(v — u)
Before t = 0, particle is at rest, hence u = 0
After t = 0, particle is moving with a constant velocity.
Velocity of the particle = slope of position-time graph
=3 m/4s =0.75 m/s
Impulse. = change in momentum = 4 (0.75 - 0) = 3 kg-m/s
(b) Impulse at t = 4 s
Before t = 4 s, particle is moving with a constant speed, u = 0.75 m/s
After t = 4s, particle is again at rest
.’. v = 0
.’. Impulse = change in momentum = m(v -u)
= 4(0-0.75)=-3 kg-m/s