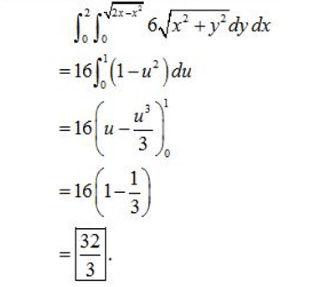Evaluate the iterated integral by converting to polar coordinates.
![]()
Answer:
Consider the following iterated integral:
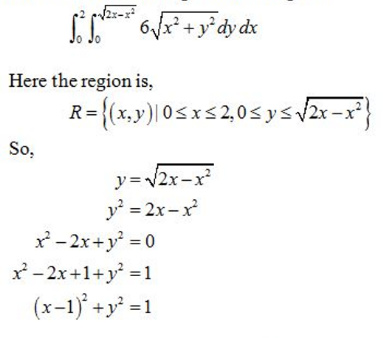
That is, the region is the top half of the disk centered at (O, 1) with radius 1.
The polar coordinates for region R is
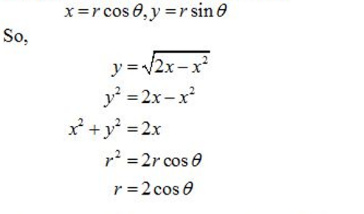
The region of in tegration in polar coordinates as,
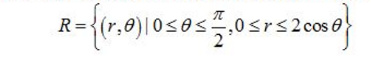
Therefore, the given integral becomes,
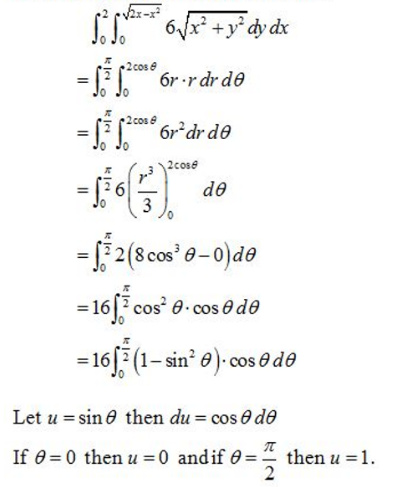
Hence the above integral becomes,