A point charge of magnitude q is at the center of a cube with sides of length L.
a- What is the electric flux Φ through each of the six faces of the cube?
b- What would be the flux Φ1 through a face of the cube if its sides were of length L1?
Concepts and reason
The concept required to solve this question is the Gauss’s law.
First calculate the electric flux through the cube. Then, calculate the electric flux through a side of the cube. Also, check whether the flux through a closed surface is depending upon the shape or size of the body.
Fundamentals
The electric flux is defined as the number of electric field lines crosses a virtual surface. The number of lines through a closed surface is independent of the shape or size of the closed surface because the electric field lines are because of charge present inside the surface.
The Gauss’s law states that the electric flux through a surface is equal to the ratio charged enclosed in the surface and the permittivity of the free space. That is,
![]()
Here, q is the charge, ![]() is the permittivity of the free space.
is the permittivity of the free space.
Answer:
(a)
Calculate the magnitude of the electric flux through each face of the cube.
The magnitude of charge enclosed by the cube is q. The cube has six equal faces, so the magnitude of electric flux through each cube is,
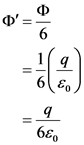

Explanation:
The charge is placed at the center of the cube. So, it is symmetric from each face of the cube. Thus, the magnitude of electric flux through each face of the cube is one sixth of the electric flux through the cube.
(b)
Calculate the magnitude of the electric flux through each face of the cube of side ![]() .
.
The number of lines through a closed surface is independent of the shape or size of the closed surface because the electric field lines are because of charge present inside the surface.
The expression for the magnitude of the electric flux through a closed surface is,
![]()
From the above relation, it is clear that the electric flux through the cube is not depending on the length of each side of the cube. So, the magnitude of electric flux through each face of the cube of side is ![]() ,
,
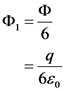

Explanation:
The electric flux through each face of the cube is independent on length of each face of the cube.