A common graphical representation of motion along a straight line is the v vs. t graph, that is, the graph of (instantaneous) velocity as a function of time. In this graph, time t is plotted on the horizontal axis and velocity v on the vertical axis. Note that by definition, velocity and acceleration are vector quantities. In straight-line motion, however, these vectors have only a single nonzero component in the direction of motion. Thus, in this problem, we will call v the velocity and a the acceleration, even though they are really the components of the velocity and acceleration vectors in the direction of motion, respectively.
Part A
What is the initial velocity of the particle, v0?
Part B
What is the total distance Δx traveled by the particle?
Part C
What is the average acceleration aav of the particle over the first 20.0 seconds?
Part D
What is the instantaneous acceleration a of the particle at t=45.0s?
a =
What is the instantaneous acceleration of the particle at ?

Which of the graphs shown below is the correct acceleration vs. time plot for the motion described in the previous parts?
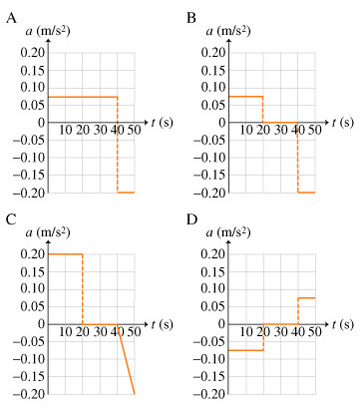
Answer:
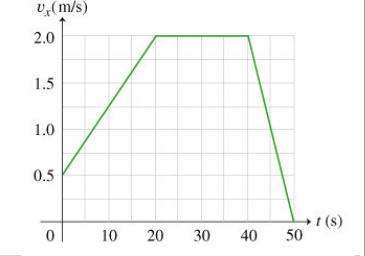
Is the above v vs t diagram as as per your question?
If yes, then ans are as follows?
a) Initial speed i.e. at t=0, v=0.5 m/s
b)Total distance travelled =Area of the region under the v vs. t curve
=the distance traveled in the first 20.0 seconds +the distance traveled in the second 20.0 seconds +the distance traveled in the last 10.0 seconds
=25+40+10
Total distance=75m
c) In a v vs. t graph, then, the average acceleration equals the slope of the line connecting the two points representing the initial and final velocities.
![]()
d) The instantaneous acceleration of a particle at any point on a v vs. t graph is the slope of the line tangent to the curve at that point.
As it is straight line, acceleration is constant
![]()
e) For graph of a vs t graph, finding the accelation for first 20 sec, second 20 sec and then last -10 sec
so , option B is correct.