A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.1 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(i) total torque on the coil,
(ii) total force on the coil
(iii) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area ${{10}^{-5}}$ ${{m}^{2}}$ and the free electron density in copper is given to be about ${{10}^{29}}$/${{m}^{3}}$).
Given, number of turns, =20
Radius of circular coil, r = 10cm =0.1 m
Magnitude of magnetic field, 5 = 0.1 T
The angle between the area vector and magnetic field is 0°.
θ=0°
Current in the coil, I = 5.0 A
(i)Torque on the coil, τ = nIAB sin θ
= 20 x 5 x \pi(0.1 x 0.1) x 0.1 x sin 0° = 0
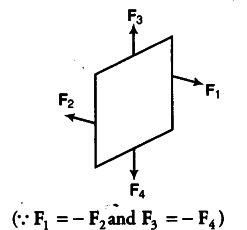
(ii) The forces on the planar loop are in pairs, i.e. the forces on two opposite sides are equal and opposite to each other and on the other two opposite sides, they are same. Thus, the total force on the coil is zero.
(iii) Number density of electrons N = {{10}^{29}}/{{m}^{3}}
Area of cross-section of copper wire, A = ${{10}^{-5}}$${{m}^{2}}
magnitude of magnetic force, F = e({ V }{ d } x B)
I = neA { V }{ d }
{ V }_{ d } = I/neA
F = e.I/NeA . B sin 90°
= 0.1 x 5 / {{10}^{-5}} x {{10}^{29}} N
= 5 x {{10}^{-25}}$